Many objects in CW4 have a rotation which can either be obtained or set through 4RPL commands. This includes the rotation of the camera, units and the individual objects custom unit is made up of. These rotations are defined in degrees, whereas the trigonometric functions of 4rpl use radians. Even though 4RPL has built in function to convert between degrees and radians, you'll still notice that a downward angle you calculated will make the camera look upwards instead. This is because the game uses a rotation system specific to the Unity engine that doesn't match with how rotations are usually calculated along axes in maths.

This page will show you how the different types of rotations in this game work and how to convert between them

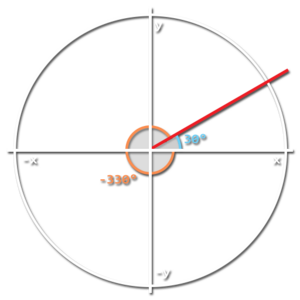You're probably at least a little familiar with a coordinate grid as show here, with an X and Y axis. An arbitrary angle is usually defined by the distance in radians or degrees from the positive side of the X-axis. You can define the same angle with both a positive or negative value, 30° is the same as -330°. (in radians: ⅙π and -1⅚π)

The trigonometry functions of 4RPL such as sin, cos, tan, atan2, etc. all use or return radian values, but other parts of the game use degrees, which is why you'll have to convert between them.

In school you may have learned a formula of how to convert radians to degrees and vice versa, but that is not necessary in 4RPL. Simply multiply your angle by either the rad2deg or deg2rad constant:

# Don't do this
<-radAngle PI / 180 * ->degAngle
<-degAngle 180 / PI * ->radAngle
 
# Do this
<-radAngle rad2deg * ->degAngle
<-degAngle deg2rad * ->radAngle

TLDR; Rotations along the X and Y axes are inverted.

Even though units are normally locked to the grid, the game allows us to rotate them by any amount. Lets try to give a unit a Y rotation of 30°, which should make them point slightly up and to the right, just like the image above here.

GetSelectedUnits [0] ->unit        # Get the first selected unit
SetUnitRotation(<-unit V3(0 30 0)) # Set the new rotation

What we see when we run this however, is that the unit faces down and to the right instead, we only get the result we originally expected when we use the negative value -30°. This means that rotations along the Y-axis is inverted. It turns out the the same is true for the X-axis. The Z axis on the other hand is fine and works as we would expect.

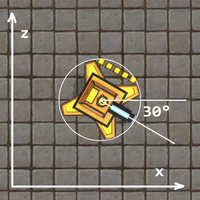
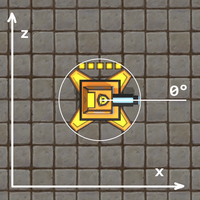
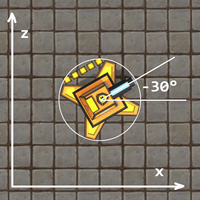Rotating along the Y-axis is inverted

So, if you work out some kind of angle within the map's coordinate system and you want to to use that angle to modify a unit in some way, make sure to invert the X and Y axes before doing so, or your unit will turn in exactly the opposite way. The easiest way to invert the X and Y angles of a vector is as follows: <-rotVector V3(-1 -1 1) * ->rotVector

TLDR; Camera is offset to the left by 90°

The camera also uses the same rotation we discussed before where the X and Y axes are inverted, but it has another problem. When the camera is rotated 0° on all axes, it faces forward in the direction of the Z axis. We've seen above that units such as cannons face to the right when they are rotated 0°, the camera facing a different direction at 0° actually messes with things. It is already rotated 90° further to the left than usual, which means that when we calculate an angle and set the camera to this rotation, it will always end up facing 90° to the left of where we actually pointed our angle.

To account for this, we'll have to turn our angle 90° to the right before setting the camera. Similarly, when we want to convert the angle back into something that works in the map's coordinate system, you'll have to turn 90° left first. Below are some functions made for converting from and to camera orientation.

# inverts the X and Y axes of a vector
:invXY # v1 - v2
    V3(-1 -1 1) * # multiply x and y with -1
 
# converts from a radian math rotation to a camera rotation vector
:rad2cam # v1 - v2
    rad2deg * 
    @invXY 
    V2(0 90) + # turn right 90°
 
# converts from a camera rotation to a radian math rotation vector
:cam2rad # v1 - v2
    V2(0 90) - # turn left 90°
    @invXY 
    deg2rad *